Tap for more steps Split the limit using the Sum of Limits Rule on the limit as x x approaches 0 0 1 2 ⋅ lim x → 0 1 lim x → 0 cos ( x) lim x → 0 sin 2 ( x) 1 2 ⋅ lim x → 0 1 − lim x → 0 cos ( x) lim x → 0 sin 2 ( x) Move the limit inside the trig function because cosine is continuousTaking the numerator and denominator separately and letting x approach 0, sinx = 0 and x=0, this will be of the form 0/0 which stands undefined There is a proof which involves the left limit and the right limit which will work out to1 However, o By using the Squeeze Theorem lim x→0 sinx x = lim x→0cosx = lim x→01 = 1 lim x → 0 sin x x = lim x → 0 cos x = lim x → 0 1 = 1 we conclude that lim x→0 sinx x = 1 lim x → 0
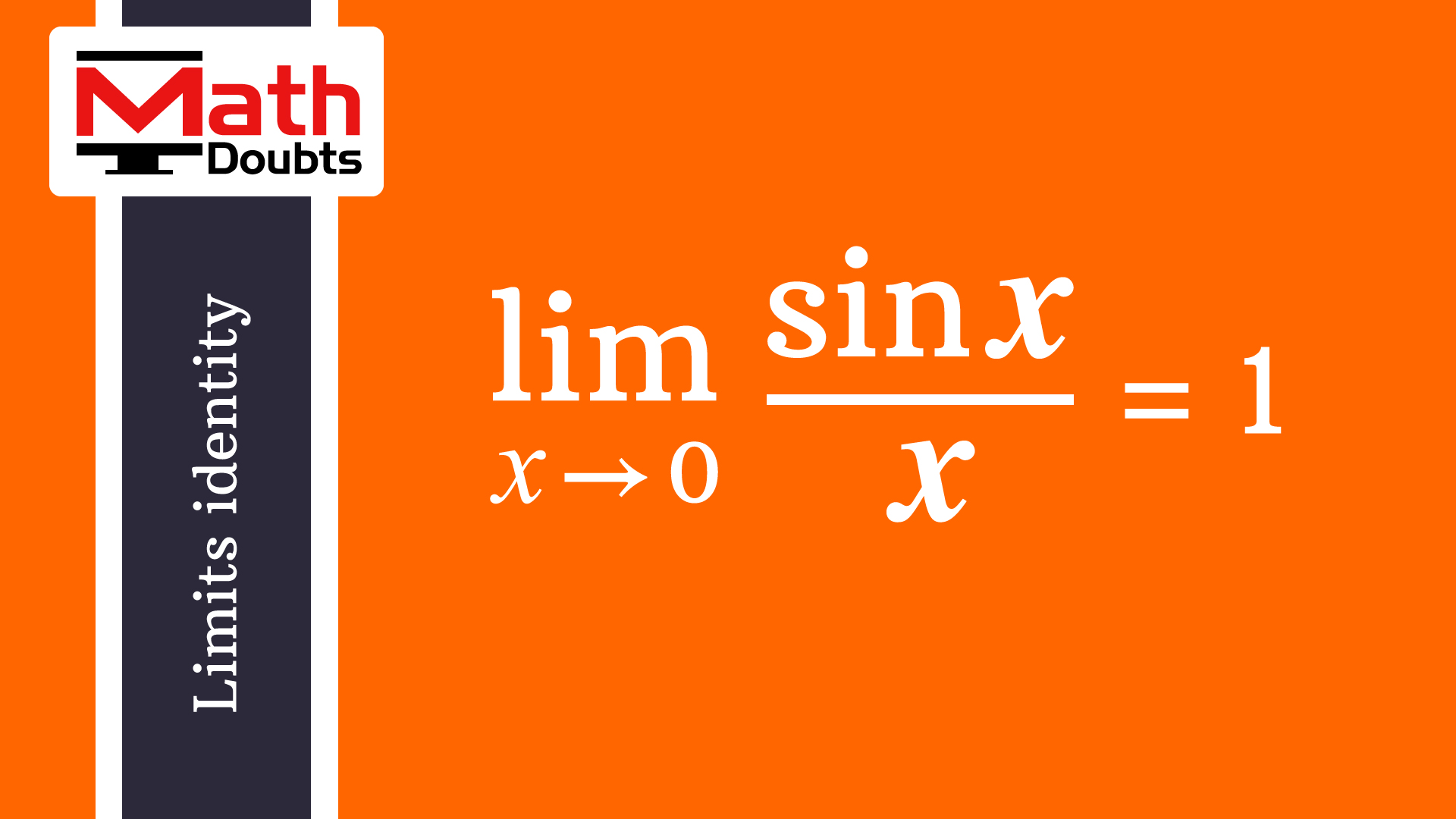
Lim X 0 Sinx X Formula
Lim x → 0 sinx/x(1+cosx) is equal to
Lim x → 0 sinx/x(1+cosx) is equal to-Sinx/x limit as x approaches 0 shall become lim cosx/x as x approaches 0 Again checking the value in expression, cos0=1 and x=1, 1/1=1 Therefore, this limit works out to 1 Similarly, tanx/x limit as x approaches 0 is also 1 It should be borne in mind that x $$\lim_{x \to 0} \frac{\sin x}{2x\cos x^2} = \left(\lim_{x \to 0} \frac{\sin x}{x}\right)\left(\lim_{x \to 0} \frac{1}{2\cos x^2}\right)$$ which you can do if the limits exist So while it looked like L'Hopital's rule was only being applied to part of the fraction, namely, the sin x/x part, it really wasn't



How To Evaluate Lim X 0 1 Cosx Xsinx Quora
How you show that itex\lim_{x\to 0} sin(x)/x= 1/itex depends upon exactly how you have defined sin(x)!Lim x→∞√ xsinx x−cosx = lim x→∞ x1 2√1sinx x x1 2√1−cosx x We know, that for any value of x, sinx and cosx will be 1,1 So, = lim x→∞ Sinx x = 0 And = lim x→∞ Cosx x = 0 = x1 2√1 sinx x √1sinx x √1cosx x = lim x→∞ 1 1 = 1 Related QuestionsSOLUTION lim x→0 2sinx−sin2x x3 = lim x→0 2sinx(1−cosx)(1cosx) x3(1cosx) = lim x→02sin3x x3 × 1 1cosx
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW the value of `lim_(x gt0)(cos(sinx)cosx)/x^4` is equal toA common limit seen in Calculus This video show the limit of (1cosx)/x as x approaches 0 is 0 This proof uses a previous proof limit of sinx/x as x approNow, the distributive property can be used for distributing one by square root of two over the subtraction of the sine and cosine functions = lim x → π 4 ( 2 × 1 2 × sin x − 1 2 × cos x x − π 4) According to the trigonometry, the sine of angle 45 degrees and cosine of angle forty five degrees are equal to the
Take the limit of each term Tap for more steps Split the limit using the Sum of Limits Rule on the limit as x x approaches 0 0 0 lim x → 0 1 − lim x → 0 cos ( x) 0 lim x → 0 1 lim x → 0 cos ( x) Move the limit inside the trig function because cosine is continuousSal was trying to prove that the limit of sin x/x as x approaches zero To prove this, we'd need to consider values of x approaching 0 from both the positive and the negative side So, for the sake of simplicity, he cares about the values of x approaching 0 in the interval (pi/2, pi/2), which approach 0 from both the negative (pi/2, 0) andNow, split the function as the product of following two functions by factorization = lim x → 0 ( tan x x × ( 1 − cos x) x 2) Use product rule of limits to find the limit of the function by the product of their limits = lim x → 0 tan




Finding The Limit Of 1 Cos X X Video Lesson Transcript Study Com



Http Math Hws Edu Mitchell Math130f12 Tufte Latex Triglimits
An important limit to know with a few tricky steps Follow our stepbystep solution to (cos(x) 1) / x to get a good understandingD(sinx)/dx/d(x(1cosx))/dx = Cosx/(1cosx xsinx ) Now check whether 0/0 form removed or not if not then again repeat differentiation of num and denominator In this question we removed 0/0 form by applying L'Hôpital's rule one time Last step putting x=0 =1/(11–0) =1/2(fin1 Definition of a Limit lim x>c f(x) = L The limit of f(x) is the value that f(x) gets close to, as x gets close to some number c we say "the limit of f(x) as x approaches c is L" lim x>c f(x) "the limit of f(x) as x approaches c from the r" (x starts bigger than c but gets smaller towards c) "the limit of f(x) as x approaches c from



Evaluate Lim X 0 1 Cos X Cos2x Cos3x Sin 22x Sarthaks Econnect Largest Online Education Community




Evaluate X 0 2 1 Cosx Sin 2x
X is a common factor in the each term of the trigonometric expression in the numerator So, take it common from them for simplifying this trigonometric expression further = 1 2 ( lim x → 0 sin 2 x ( 3 − 2 sin 2 x) x 2) Now, factorise this algebraic trigonometric function as follows = 1 2 ( lim x → 0Solved example of limits lim x → 0 ( 1 − cos ( x) x 2) \lim_ {x\to0}\left (\frac {1\cos\left (x\right)} {x^2}\right) x→0lim ( x21−cos(x) ) Intermediate steps Plug in the value 0 0 0 into the limitThis is a proof of the limit of sinx/x as x approaches 0 from the positive side The squeeze theorem is used to squish sinx/x between two values that approa




The Function F X Sinx X Cosx X 0 And F X K X 0 Is Continuous At X 0 Then Find The Value Of K




Indeterminate Forms Recall That In Some Cases Attempting To Evaluate A Limit Using Substitution Yields An Indeterminate Form Such As 0 0 Usually We Ppt Download
Recall that the quadratic approximations of sin x and cos x near x = 0 are cos x ≈ 1 sin x ≈ x Thus, sin x x lim lim x→0 1 − cos x ≈ x→0 1 − 1 x = lim x→0 0 Replacing cos x by its linear approximation makes the denominator equal to 0 We begin to have some idea that this rational function is lim_(x rarr 0) (1 cosx)/(x sinx) = 1/2 First of all, since as x rarr 0, sinx rarr 0 also, we can rewrite the denominator as x^2 Hence we need to find lim_(x rarr 0) (1 cosx)/(x^2) Since this still results in an indeterminate 0/0, we apply L'Hopital's Rule (d/dx(1cos x)) / (d/dx(x^2)) = sinx/(2x) If we substitute 'approaching zero' as a less formal 1/oo, we arrive at the expression (1/oo)/(2/oo) After cancelling out the infinities, this leaves 1Click here👆to get an answer to your question ️ x→0^ ( (xcosx)^x (cosx)^1/ x (xsinx)^x ) is equal to




Sandwich Theorem And Trigonometric Functions Proof Videos Examples



Prove Limit Of Sin X X Is 1 And Limit Of Chegg Com
Lim x → 0 sin ( π cos 2 x) x 2 It's very important to simplify the trigonometric function before finding its limit as x tends to 0 It can be done by using two basic trigonometric identities According to cos squared formula, the square of cos function can be expanded in terms of square of sin function = lim x → 0 sin Solve for x sin^1x cos^1x = 0, where x is a non negative real number and , denotes the greatest integer function asked in Sets, relations and functions by SumanMandal ( 546k points) x ⋅ cos ( 1 x) ≤ sin x and since sin x → 0 by squeeze theorem the limit is equal to 0 For x < 0 we can use a similar argument




Limit 1 Cosx X 2 At Times L Hospital S Rule May Not Be Applied Youtube



What Is The Limit Of 1 Cosx Cos2x X Quora
Click here👆to get an answer to your question ️ x→0(1 cos2x)(3 cosx) xtan4x is equal to Join / Login >> Class 11 >> Applied Mathematics >> Limits and Continuity >> Methods of evaluating limit of a function The value of x → 0 lim x 3 1 sin x − cos x lo g (1L'Hopital's rule is a mathematical rule explaining that the limit as x approaches C of two functions, f(x) and g(x), both approaching zero, is equal to the limit as x approaches C of the functions We can use L'Hopital's Rule now Get the derivatives of both the numerator and denominator 5" "=e^(lim_(x>0)(sinx/cosx)/(2x))=e^(lim_(x>0)(sinx/(2xcosx)) This is still indeterminate so you must apply L'Hopital's Rule again 6" "=e^(lim_(x>0)(cosx/(2(xsinxcosx))) You can now get the limit by substitution



Find The Limit As X Goes To 0 Of Cos Sin X Cos X X4 Stumbling Robot




Lim X Tends To 0 1 Cos 3 X X Sinx Cosx Brainly In
Evaluate ∫(xsinx)/(1 cos2x)dx for x →0, π Consider the integral I = ∫ xsinx \1 cos^2x dx, x∈0,π (i) Express I = π/2 ∫ sinx/1 cos^2x dx, x∈0,π (ii) Show that I = π^2/4It is time to concentrate on finding the limit of the remaining function = lim x → 0 cos ( sin x) − 1 x 2 The trigonometric expression in the numerator represents one minus cosine of angle trigonometric formula and it is useful to convert the expression into sine function There is a limit rule in terms of sineClick here👆to get an answer to your question ️ x→0 1 cos(1 cosx)/x^4 = Join / Login > 11th > Maths lim x → 0 (tan (5 x) sin x View solution x → 3 π lim 2 c o s x − 1 s i n (3 π − x) is equal to Medium View solution View more Learn with content Watch learning videos, swipe through stories, and browse through



What Is The Limit Of 1 Cosx Cos2x X Quora




Ex 13 1 18 Evaluate Lim X 0 Ax X Cos X B Sin X Ex 13 1
on solving lim x → ∞ x sin ( x) / ( x − cos 2 ( x)) I divided by x in both numerator and denominator and since lim x → ∞ s i n ( x) / x = 0 and lim x → ∞ c o s ( x) / x = 0 i arrive at lim x → ∞ 1 / 1 − 0 ∞ but this limit can not be written as equal to 1,because this is indeterminate form so how should i proceed further? If lim (x→0) ((x sin x – x cos x – tanx)/x^n) exists and have a nonzero finite value, then find n asked in Limit, continuity and differentiability by SumanMandal ( In my book, this limit $$\lim_{n\to\infty}n\left(\sin x\right)^{2n1}\cos x=0$$ is used to solve an integration problem But I want to figure out how this limit works out What special limit is used to derive it or is it itself a special limit




Limit Of Trig Function By Rationalizing Xsinx 1 Cosx Youtube



What Is The Value Of Lim X Tends To Zero Sinx X Quora
Evaluate ( limit as x approaches 0 of sin(2x))/(sin(x)) Multiply the numerator and denominator by Multiply the numerator and denominator by L'Hospital's Rule states that the limit of a quotient of functions is equal to the limit of the quotient of their derivatives Find the derivative of the numerator and denominatorDisplaystyle limx → 0 (cos xsin x)(1/x) equals (A) e1 (B) e1 1 (D) 0 Check Answer and Solution for above question from Mathematics in Limit8 Answers8 Hint Try using lim x → 0(1 x − 1 sinx) = lim x → 0(sinx − x xsinx) and apply L'Hopital's rule For fun, and because of the precalculus tag, we give a proof without calculus It turns out that there is a geometric argument that x − sinx is less than a constant times x3 for x near 0



What Is Lim Sinx X As X Approaches 0 Quora




Limit Of 1 Cos X X As X Approaches 0 Youtube
X→0lim (cosxasinbx)x1 is of form 1∞, so its limit will be ek, wherek = x→0lim x1 (cosxasinbx−1) = x→0lim 1−sinxabcosbx = ab =2Hence all possible combination of a and bEvaluate limit as x approaches 0 of (sin(2x))/x Evaluate the limit of the numerator and the limit of the denominator L'Hospital's Rule states that the limit of a quotient of functions is equal to the limit of the quotient of their derivatives Move the limit inside the trig function because cosine isMost calculus texts define sine and cosine in terms of coordinates on the unit circle, then give a rather handwaving geometric argument




Lim X 0 Sin Cosx 1 Cosx Where Denotes Greatest Integer Function Equal To A 1 B Sin1 Youtube



Use Of Infinitesimals
Value of sine and cosine is always lies between 1 to 1 so here the greatest term is x as x is tending to infinity in order to get the limiting value of this expression we have to divide numerater as well as denominator by the greatest term ie x one division is done put the limit and get the answerhence and is equal to 1 Let f(x) = (cos x, x, 1) (2 sin x, x2, 2x) (tan x, x, 1) then lim(x → 0) f'(x)/x is equal to (a) 0 (b) 1 (c) 2 (d) 2 Let f(x) = {k cos x/(π 2x), where x ≠ π/2, 3 , where x ≠ π/2 and if lim(x → π/2) f(x) = f(π/2), find the value of kLimit of xsin(x)/(1 cos(x)) Calculus Limits Involving sin(x)/x with the Mayan Statue




What S The Evaluation Of Lim X 0 Xtanx 1 Cosx Quora




How To Show That 1 Cosx X 2 P For 0 X P 2 Quora
Find limit of sin x / (1 cos x) as x > 0 I'm thinking I want to change 1 cos x into an x somehow However, if I do a table of values, I show the limit heading towards infinity on the right side of zero and the limit heading towards negative infinity on the left side of zeroShowing that the limit of (1cos(x))/x as x approaches 0 is equal to 0 This will be useful for proving the derivative of sin(x)Watch the next lesson https Evaluate lim x →0 (1 sinx)cot x Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to



What Is The Limit Of X Sinx X Cosx When X Tends To Infinity Quora




For Xgt0 Lim Xto0 Sinx 1 X 1 X Sinx Is
The value of x → 0 lim x 4 cos (sin x) − cos x is equal to A 5 1 B 6 1 C 4 1 D 2 1 Medium Open in App Solution Verified by Toppr Correct option is B 6 1 x → 0 lim x 4 cos (sin x) − cos x = x → 0 limNo need for L'Hopital's Recall the definition of the derivative mathf'(a) = \lim_{\Delta x \to 0} \frac{f(a\Delta x)f(a)}{\Delta x}/math From setting




The Value Of Lim X 0 Sinx X 1 1 Cosx




Calculus Limit Problem 1 Cosx Sinx As X Approaches 0 Youtube




Lim Tanx Sinx X 1 Cos2x X Gt 0 Brainly In




Evaluate Lim Xto0 Sqrt 2 Sqrt 1 Cosx Sin 2 X




Ex 13 1 17 Evaluate Lim X 0 Cos2x 1 Cosx 1 Ex 13 1




Lim X To 0 2 Tan X 2 Sin X X 2 Sin X Without L Hopital S Rule How Is My Procedure Wrong Mathematics Stack Exchange




Lim X Approaches 0 Xcosx Sinx X 2sinx Is Equal To Brainly In




न क ल Lim X To 0 Tanx Sinx 1 Cosx
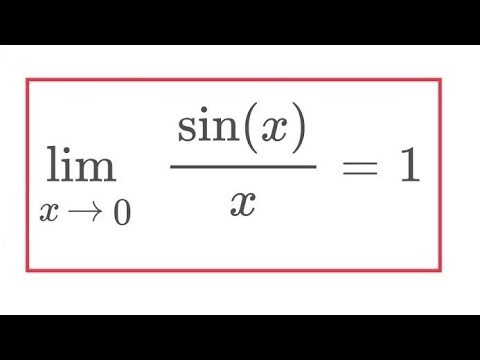



Lim Sin X X 1 As X Goes To 0 Youtube
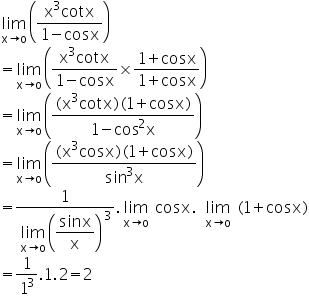



Lim X3 Cotx 1 Cosx X 0 Mathematics Topperlearning Com Ruzmb7jj




If Lim X 0 1 Cos 1 Cos X 2 2 M X N Is Equal To The Left Hand Derivative Of F X E X At X 0 Then The Value Of N M Is




If F X Int X Sinx 1 Cosx Dx And F 0 0 Then The Value Of F Pi 2 Is




Ex 7 11 15 Evaluate Sin X Cos X 1 Sin X Cos X Dx
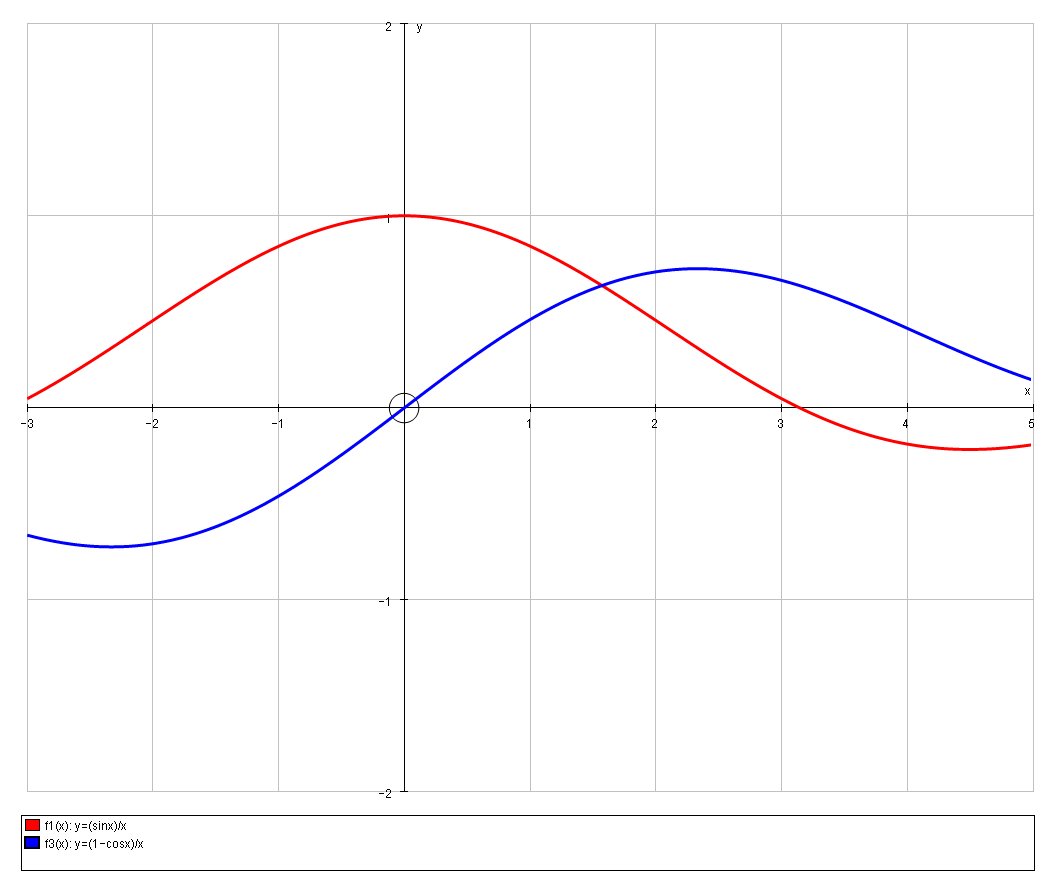



Consider The Function Defined By F X Sinx X If 1 X 0 Ax B If 0 X 1 And 1 Cosx X If X 1 How Do You Determine A And B Such



Dejkfunywey44m




Is The Usual Proof Of Lim X Rightarrow 0 Frac Sin X X 1 An Honest Proof Mathematics Stack Exchange



If Lim X 0 1 Sinx Cos X Log 1 X Xtan 2x Exists And Is Equal To M N Find The Value Of M N Sarthaks Econnect Largest Online Education Community



Lim Sin 2 X 2 1 Cos X Equals Sarthaks Econnect Largest Online Education Community




What Is The Limit Of 1 Cosx X As X Approaches 0 Quora




Finding The Limit Of 1 Cos X X Video Lesson Transcript Study Com



Evaluate The Limit Limx P 2 Cos 2 X 1 Sin X Sarthaks Econnect Largest Online Education Community




Lim X 0 1 Sinx Cosx Ln 1 X X Tan 2x




What S The Evaluation Of Lim X 0 Xtanx 1 Cosx Quora



Sin X Cos X 1 How To Find X Quora
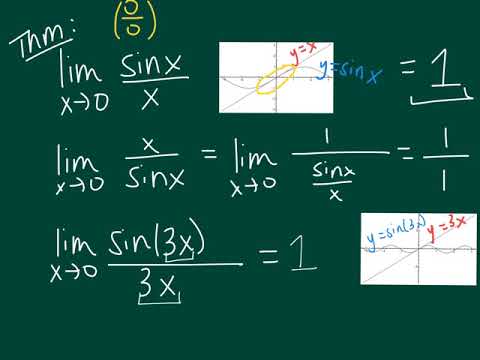



Limit Of Sin X Over X As X Approaches 0 Youtube




Find The Value Of Lim X 0 1 Cosx Xsinx Youtube



What Is The Limit Of 1 Cosx X As X Approaches 0 Quora




Limit Of Sin X Cos 1 X As X To 0 Mathematics Stack Exchange




Finding The Limit Of 1 Cos X X Video Lesson Transcript Study Com




Limit X Tends To 0 1 Cos X X 2 Evaluate The Limit Brainly In




Evaluate Lim X 0 1 Cosx Cos2x X




Proof Of Limit Of Sin X X 1 As X Approaches 0 Math Linux Com




Show That The Function F X Defined By F X Sinx X Cosx X 0 F X 4 1 The Whole Root Of 1 X X X 0 Is Continuous At X 0 Mathematics Topperlearning Com 9hfmr6kk
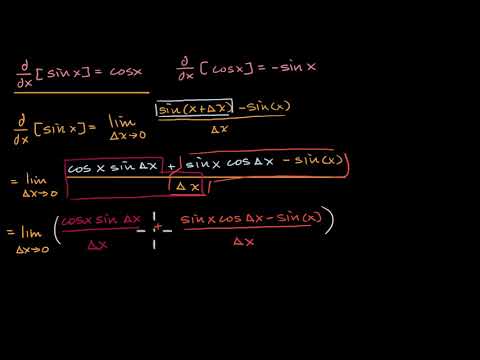



Proof Of The Derivative Of Sin X Video Khan Academy




Lim X To 0 X Cos X Sin X X 2 Sin X क म न ज ञ त क ज ए Youtube




Evaluating Lim Limits X To Pi Frac Pi X Sin X 1 Cos X Mathematics Stack Exchange
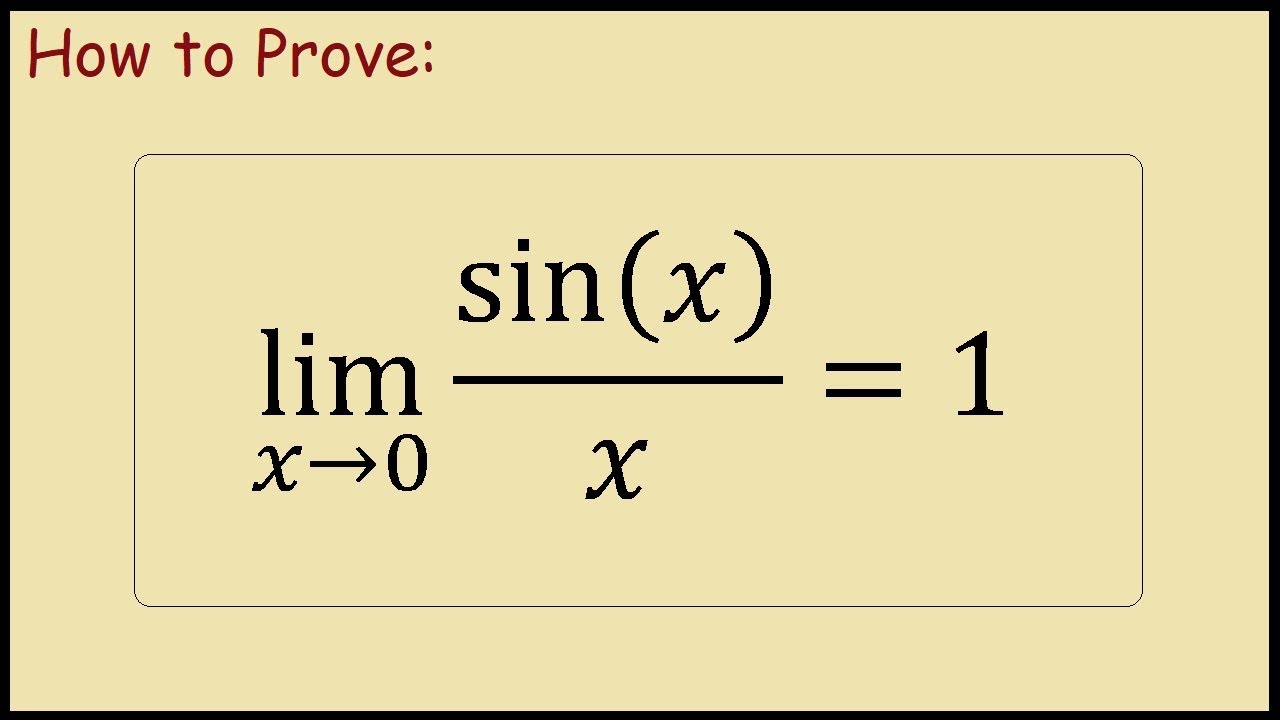



Prove Lim Sin X X 1 As X Approaches 0 Squeeze Theorem Youtube




Why Does The Inequality 0 Cos X Sin X X 1 Hold True In The Interval 𝛑 2 𝛑 2 Mathematics Stack Exchange




Lim X Gtpi Sqrt 1 Cosx Sqrt 2 Sin 2x Youtube



Www Amherst Edu Media View Original Ma11fall09finalanswers Pdf




Q109 Limit Of Cos X 1 Sin X Youtube



Q Tbn And9gct1on0v06ru3be5zp10b5ft94umzeku7dgfp8mjl Tvanliyfl5 Usqp Cau



How To Evaluate Lim X 0 1 Cosx Xsinx Quora



Limx 0 Sin X 1 Cos X X 3 Sarthaks Econnect Largest Online Education Community




Evaluate X 0x Sinxcosx X 3



Dqlksw9mhn1ukm




Limit Of Xsin X 1 Cos X Calculus Limits Involving Sin X X With The Mayan Statue Youtube



What Is Limit X 0 Xcosx Sinx Quora



What Will Be The Value Of Limit X 0 1 Cosx X 2 Quora




Finding The Limit Of 1 Cos X X Video Lesson Transcript Study Com



How To Solve The Limit Without L Hopital Math Displaystyle Lim X To Frac Pi 3 Frac Sin X Frac Pi 3 1 2 Cos X Math Quora




Find The Limit Lim X Pi 4 Of Sin X Cos X Cos 2x Youtube



1
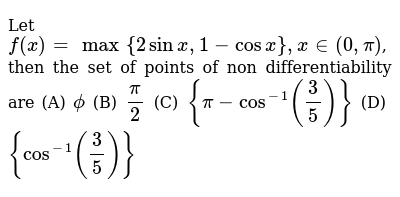



Let F X Max 2 Sin X 1 Cos X X In 0 Pi Then The Set Of Points Of Non Differentiability Are A Phi B Pi 2 C Pi Cos 1 3 5 D Cos 1 3 5



What Is The Limit X 0 If Tan X Sin X X 3 Quora




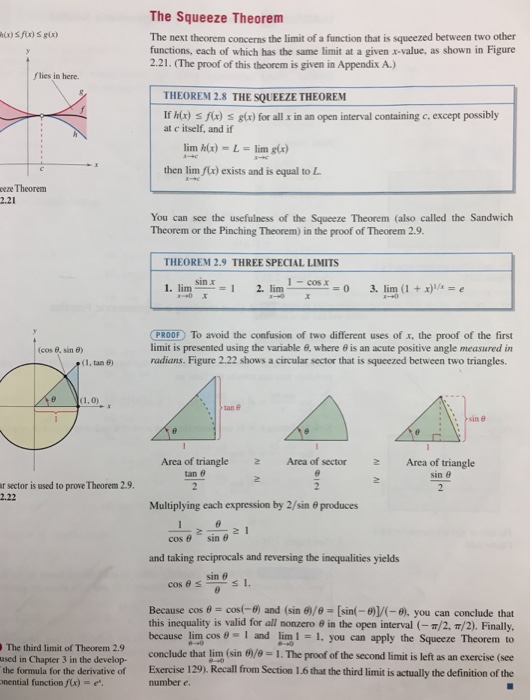
The Squeeze Theorem




Evaluate X 0 X Tan 4x1 Cos 4x



Limx 0 Sin Cos X 1 Cos X Denotes The Greatest Integer Function Is Equal To Sarthaks Econnect Largest Online Education Community




Ex 13 1 17 Evaluate Lim X 0 Cos2x 1 Cosx 1 Ex 13 1



1



1



Lim X 0 Sinx X Formula



Users Math Msu Edu Users Zhan Hw13 Solution Pdf




Limit Of 1 Cos X X As X Approaches 0 Video Khan Academy




L Hopital S Rule Limit At 0 Example Video Khan Academy




If F X Sqrt X Sinx X Cos 2x Then Lim X Oo F X Is



Limit Of Sin X 2 Y 2 X 2 Y 2 Using Polar Coordinates And L Hopital S Rule Youtube




Prove The Limit As X Approaches 0 Of 1 Cos X X Youtube




Limit Of Cos X 1 Sin X Calculus 1 Trig Limits Youtube




Limits At Infinity Of Quotients With Trig Video Khan Academy




Lim Xrarr0 Sinx Sqrt X 1 Sqrt 1 X Is Equal To




The Value Of X 0 Sin 1 Sinx Cos 1 Cosx 2tan 1 Tanx Is Equal To




Lim X 0 2 7 X 9 X 3 X 1 Sqrt 2 Sqrt 1 Cosx
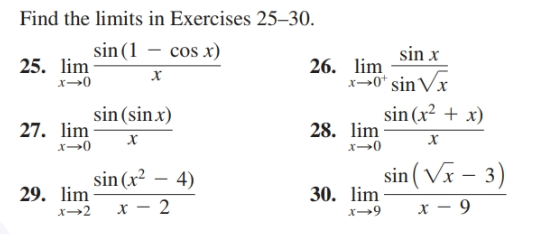



Answered Find The Limits In Exercises 25 30 Sin Bartleby



Dqlksw9mhn1ukm
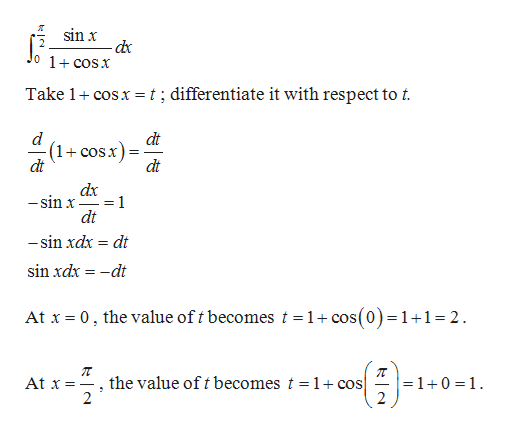



Answered In Solving The Integration Of Sin X Bartleby




Important Trig Limit With Tanx Sinx Sin 3x Youtube




Limit Of Sin X X As X Approaches 0 Video Khan Academy



Can You Prove That The Limit Of X Sinx 1 Cosx Is 1 As X Approaches 0 Quora




The Value Of Lim X Gt0 Sinx 1 X 1 X Sinx Youtube



0 件のコメント:
コメントを投稿